In the early stage of algorithm design, the goal was to solve exacly and efficiently the combinatorial problems. Cook’s Theorem and the NP-completeness theory showed us that some problems are inehently hard. How can we solve this problem? By trying to find approximated solutions or by trying to look at restricted instances of those problems that are tractable. It turns out that the lack of computational power (NP-hardness in some sense) is not the only obstracle to solving problems optimally. Online algorithms propose a model where the difficulty is due to lack of information. The algorithm must take some decisions before seeing the entire input. Again, in most of the cases it is hopeless to get an optimal solution (the solution we could get if we knew the input ahead of time) and our goal is not to be far from it. Other example of natural limitation are streaming algorithms, where you should solve a certain problem with limited memory. Imagine for example one algorithm that runs in a router, that received gigabits each second. It is impossible to store all the information, and yet, we want to process this very very large input and give an anwer at some point.
An additional model is inspired in economy: there are a bunch of agents which have part of the input to the algorithm and they are interested in the solution, say, they have a certain value for each final outcome. Now, they will release their part of the input. The may lie about it to manipulate the final result according to their own interest. How to prevent that? We need to augment the algorithm with some economic incentives to make sure they don’t harm the final solution too much. We need to care about two things now: we still want a solution not to far from the optimal, but we also need to provide incentives. Such algorithm with incentives is called a mechanism and this represents one important field in Algorithmic Game Theory called Mechanism Design.
The simplest setting where this can occur is in a matching problem. Suppose there are  people and one item. I want to decide which person will get the item. Person
people and one item. I want to decide which person will get the item. Person 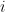 has a value of
has a value of  of the item. Then I ask people their values and give the item to the person that has a higher value and this way I maximize the total cost of the matching. But wait, this is a not a mechanism yet. People don’t have incentives to play truthfully in this game. They may want to report higher valuations to get the item. The natural solution is to charge some payment
of the item. Then I ask people their values and give the item to the person that has a higher value and this way I maximize the total cost of the matching. But wait, this is a not a mechanism yet. People don’t have incentives to play truthfully in this game. They may want to report higher valuations to get the item. The natural solution is to charge some payment 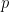 from whoever gets the item. But how much to charge? The solution is the Vickrey auction, where we charge the second highest bid to the winner. More about Vickrey auction and some other examples of truthful mechanisms can be found in the Algorithmic Game Theory book, which can be found in Tim Roughgarden’s website.
from whoever gets the item. But how much to charge? The solution is the Vickrey auction, where we charge the second highest bid to the winner. More about Vickrey auction and some other examples of truthful mechanisms can be found in the Algorithmic Game Theory book, which can be found in Tim Roughgarden’s website.
One of the most famous early papers in this are is the “Optimal Design Auction” by Myerson where he discusses auctions mechanisms that maximize the profit for the seller. After reading some papers in this area, I thought I should return and read the original paper by Myerson, and it was indeed a good idea, since the paper formalizes (or makes very explicit) a lot of central concept in this area. I wanted to blog about the two main tools in mechanism design discussed in the paper: the revelation principle and the revenue equivalence theorem.
Revelation Principle
We could imagine thousands of possible ways of providing economic incentives. It seems a difficult task to look at all possible mechanisms and choose the best one. The good thing is: we don’t need to look at all kinds of mechanisms: we can look only at truthful revelation mechanisms. Let’s formalize that: consider  bidders and each has value
bidders and each has value  for getting what they want (suppose they are single parameter agents, i.e., they get
for getting what they want (suppose they are single parameter agents, i.e., they get  if they get what they want or
if they get what they want or 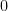 if they don’t). We can represent the final outcome as a vector
if they don’t). We can represent the final outcome as a vector ![{x \in [0,1]^n} {x \in [0,1]^n}](http://s0.wp.com/latex.php?latex=%7Bx+%5Cin+%5B0%2C1%5D%5En%7D&bg=T&fg=000000&s=0) . Here we consider also randomizes mechanisms, where the final outcome can be, for example, allocate the item to bidder
. Here we consider also randomizes mechanisms, where the final outcome can be, for example, allocate the item to bidder 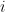 with probability
with probability  . This vector has some restrictions imposed by the structure of the problem, i.e., if there is only one item, then we must have
. This vector has some restrictions imposed by the structure of the problem, i.e., if there is only one item, then we must have  . In the end of the mechanism, each player will pay some amount to the mechanism, say
. In the end of the mechanism, each player will pay some amount to the mechanism, say  . Then at the end, player
. Then at the end, player 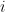 has utility:
has utility:  and the total profit of the auctioneer is
and the total profit of the auctioneer is  .
.
Let’s describe a general mechanism: in this mechanism each player has a set of strategies, say  . Each player chooses one strategy
. Each player chooses one strategy 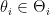 and the mechanism chooses one allocation and one payment function based on the strategies of the players.
and the mechanism chooses one allocation and one payment function based on the strategies of the players.  and
and  . Notice it includes even complicated multi-round strategies: in this case, the strategy space
. Notice it includes even complicated multi-round strategies: in this case, the strategy space  would be a very complicated description of what a player would do for each outcome of each round.
would be a very complicated description of what a player would do for each outcome of each round.
Let 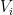 be the set of the possible valuations a player would have. So, given the mechanism, each player would pick a function
be the set of the possible valuations a player would have. So, given the mechanism, each player would pick a function 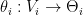 , i.e.,
, i.e., 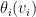 is the strategy he would pick if he observed his value was
is the strategy he would pick if he observed his value was  . This mechanism has an equilibrium if there is a set of such functions that are in an equilibrium, i.e., no one would change his function and be better off. If those exist, we can implement a this as a direct revelation mechanism. A direct revelation mechanism is a mechanism where the strategies are simply to reveal a value in
. This mechanism has an equilibrium if there is a set of such functions that are in an equilibrium, i.e., no one would change his function and be better off. If those exist, we can implement a this as a direct revelation mechanism. A direct revelation mechanism is a mechanism where the strategies are simply to reveal a value in 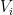 . So, I just ask each player his valuation.
. So, I just ask each player his valuation.
Given a complicated mechanism ![{x: \Theta \rightarrow [0,1]^n} {x: \Theta \rightarrow [0,1]^n}](http://s0.wp.com/latex.php?latex=%7Bx%3A+%5CTheta+%5Crightarrow+%5B0%2C1%5D%5En%7D&bg=T&fg=000000&s=0) ,
,  and equilibrium strategies
and equilibrium strategies  , I can implement this as a direct revelation mechanism just by taking:
, I can implement this as a direct revelation mechanism just by taking:

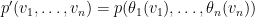
It is not hard to see that if the mechanism is 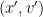 , for the players the best thing to do is to reveal directly their true valuation, eliminating all the complicated steps in between. One practical example of a direct revelation mechanism is the Vickrey auction. Consider the English auction, which is the famous auction that happens in most of movied depicting auctions (or Sotheby’s for a clear example): there is one item and people keep raising their bids untill everyone else drops and the last person still biddings gets the item. The clear strategy in those auctions is to raise your bid as long as the current value is below your valuation
, for the players the best thing to do is to reveal directly their true valuation, eliminating all the complicated steps in between. One practical example of a direct revelation mechanism is the Vickrey auction. Consider the English auction, which is the famous auction that happens in most of movied depicting auctions (or Sotheby’s for a clear example): there is one item and people keep raising their bids untill everyone else drops and the last person still biddings gets the item. The clear strategy in those auctions is to raise your bid as long as the current value is below your valuation  and there still other bidders that haven’t dropped the auction. Clearly the person with highest value
and there still other bidders that haven’t dropped the auction. Clearly the person with highest value  will get the item. Let
will get the item. Let 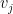 be the second highest value. It is not hard to see that all but one will drop the auction after
be the second highest value. It is not hard to see that all but one will drop the auction after 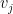 , so the highest bidders is likely to pay
, so the highest bidders is likely to pay  . This is exacly the Vickrey auction, where we just emulate the English as a direct revelation mechanism. There are of course other issues. The following quote I got from this paper:
. This is exacly the Vickrey auction, where we just emulate the English as a direct revelation mechanism. There are of course other issues. The following quote I got from this paper:
“God help us if we ever take the theater out of the auction business or anything else. It would be an awfully boring world.” (A. Alfred Taubman, Chairman, Sotheby’s Galleries)
So, we can restrict our attention to mechanims in the form ![{x : V \rightarrow [0,1]^n} {x : V \rightarrow [0,1]^n}](http://s0.wp.com/latex.php?latex=%7Bx+%3A+V+%5Crightarrow+%5B0%2C1%5D%5En%7D&bg=T&fg=000000&s=0) and
and 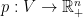 that are truthful, i.e., where the players have no incentives not to report their true valuation. We can characterize truthful auctions using the next theorem. Just a bit of notation before: let
that are truthful, i.e., where the players have no incentives not to report their true valuation. We can characterize truthful auctions using the next theorem. Just a bit of notation before: let  ,
,  , … and for
, … and for 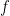 , let
, let 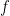 be the joint probability distribution and
be the joint probability distribution and  be the joint probability distribution over
be the joint probability distribution over  :
:
Theorem 1 An auction is truthful if and only if, for all possible probability distributions over values given by  , …,
, …,  we have
we have
-
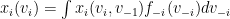 is monotone non-decreasing
is monotone non-decreasing
-
 where
where 
Revenue Equivalence
The second main tool to reason about mechanisms concerns the revenue of the mechanism: it is Myerson’s Revnue Equivalence Principle, which roughly says that the revenue under a truthful mechanism depends only on the allocation and not on the payment function. This is somehow expected by the last theorem, since we showed that when a mechanism is truthtful, the payments are totally dependent on  .
.
The profit of the auctioneer is given by 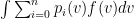 . We can substitute
. We can substitute  by the payment formula in last theorem obtaining:
by the payment formula in last theorem obtaining:

We can invert the order of the integration in the second part, getting:
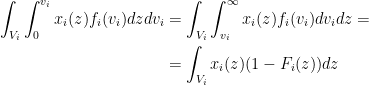
So, we can rewrite profit as:
![\displaystyle \text{profit} = \sum_{i=0}^n \int_V \left[ 1 - \frac{1 - F_i(v_i)}{f_i(v_i)} \right] x_i(v_i) f(v) dv \displaystyle \text{profit} = \sum_{i=0}^n \int_V \left[ 1 - \frac{1 - F_i(v_i)}{f_i(v_i)} \right] x_i(v_i) f(v) dv](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Ctext%7Bprofit%7D+%3D+%5Csum_%7Bi%3D0%7D%5En+%5Cint_V+%5Cleft%5B+1+-+%5Cfrac%7B1+-+F_i%28v_i%29%7D%7Bf_i%28v_i%29%7D+%5Cright%5D+x_i%28v_i%29+f%28v%29+dv+&bg=T&fg=000000&s=0)
And that proves the following result:
Theorem 2 The seller’s expected utility from a truthful direct revelation mechanism depends only on the assignment function 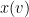 .
.
Now, to implement a revenue-maximizing mechanism we just need to find 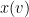 that optimize the profit functional above still meeting the truthfulness constraints in the first theorem. This is discussed by Myerson in his paper. There is just one issue here: our analysis is dependent on the probabilities
that optimize the profit functional above still meeting the truthfulness constraints in the first theorem. This is discussed by Myerson in his paper. There is just one issue here: our analysis is dependent on the probabilities  . There are various approaches to that:
. There are various approaches to that:
- Assume that the values of the bidders are drawn from distribution and
 and given to them. The distributions are public knowledge but the realization of
and given to them. The distributions are public knowledge but the realization of  is just known to bidder
is just known to bidder 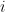 .
.
- Bidders have fixed values
 (i.e.,
(i.e.,  are the Dirac distribution concentrated on
are the Dirac distribution concentrated on  ) and in this case, the revenue maximizing problem becomes trivial. It is still an interesting problem in the point of view of truthfulness. But in this case, we should assume that
) and in this case, the revenue maximizing problem becomes trivial. It is still an interesting problem in the point of view of truthfulness. But in this case, we should assume that  is fixed but just player
is fixed but just player 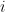 knows its value.
knows its value.
- The distributions exist but they are unknown by the mechanism designer. In this case, he wants to design a mechanism that provided good profit guaranteed against all possible distributions. The profit guarantees need to be established accourding to some benchmark. This is called prior-free mechanism design.
More references about Mechanism Design can be found in these lectures by Jason Harline, in the original Myerson paper or in the Algorithmic Game Theory book.
