Duality Theorem for Semidefinite Programming
I’ve been reading through Luca Trevisan’s blog posts about relaxations of the Sparsest Cut problem. He discusses three relaxations: (i) spectral relaxation; (ii) Leighton-Rao and (iii) Arora-Rao-Vazirani. (i) and (iii) are semi-definite programs (SDP), which is an incredibly beautiful and useful generalization of Linear Programs. This technique is the core of the famous MAX-CUT algorithm from Goemans and Williamson and was also applied to design approximation algorithms for a large variety of combinatorial problems. As for Linear Programming, there is a Duality Theorem that allows us to give certificates to lower and upper bounds. I was curious to learn more about it and my friend Ashwin suggested me those great lecture notes by Lazlo Lovasz about semi-definite programming. I was surprised that the proof of the duality theorem for SDP is almost the same as for LP, just changing a few steps. We begin by using the Convex Separation Theorem to derive a Semi-definite version of Farkas’ Lemma. We use this version of Farkas’ Lemma to prove the Duality Theorem in a similar manner that is normally done for LP. Let’s go through the proof, but first, let’s define positive semidefinite matrices:
Definition 1 A matrix
is said to be positive semidefinite (denoted by
) if for all
we have
.
It is the same as saying that all eigenvalues of are non-negative, since the smallest eigenvalue of
is given by
. We denote
when all eigenvalues of
are stricly positive. It is the same as
for all
. Also, given two matrices
and
we use the following notation:
what is nothing more than the dot-product when we see those matrices as vectors in
. Therefore:
Definition 2 A semi-definite program (SDP) is an optimization problem where the variable is a matrix
and has the form:
that is, it is a linear program and the restriction that the variable, viewed as a matrix, must be positive semi-definite.
The interesting thing is to use that the set of semi-definite matrices is a convex cone, i.e., if
then
for any
. It is easy to see this is a convex set. Now we use the following theorem to prove Farkas’ Lemma:
Theorem 3 (convex separation) Given two convex sets
such that
then there is
such that
for all
and
for all
. Besides, if one of them is a cone, it holds with
.
Theorem 4 (Semi-definite Farkas’ Lemma) Exacly one of the following problems has a solution:
,
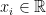
, …,
,

Proof: If problem doesn’t have a solution then the cone
is disjoint from the convex cone
and therefore they can be separated. This means that there is
(
plays the role of
in the convex separation theorem), such that:
for all
and
for all
. Now, taking
and all others
and then later
and all other zero, we can easily prove that
.
It remains to prove that . Just take
for
and then we have that
for all
and therefore,
.
Now, we can use this to prove the duality theorem. We will use a slighly different version of Farkas’ Lemma together with an elementary result in Linear Algebra. The following version comes from applying the last theorem to the matrices:
instead of .
Theorem 5 (Semi-definite Farkas’ Lemma: Inomogeneous Version) Exacly one of the following problems has a solution:
,
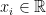
, …,
,
,

where means
. Now, an elementary Linear Algebra result before we can proceed to the proof of the duality theorem:
Theorem 6 Given two semi-definite matrices
and
we have
, where
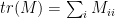
Proof: The trace of a matrix is invariant under change of basis, i.e. for any non-singular matrix , we have that
. This is very easy to see, since:
Now, we can write in the basis of ‘s eigenvectors. Let
be a matrix s.t.
where
Now:
since because the matrix is positive semi-definite and:
Now, we are ready for the Duality Theorem:
Theorem 7 (SDP Duality) The dual of the program 1 is given by:
We call 1 the primal problem and 2 the dual. If
is feasible for 1 and
is feasible for 2, then
. Besides, if the dual has a strict feasible solution (i.e. with
) then the dual optimum is attained and both have the the same optimal value.
As we can see in the theorem above, the main difference between this duality theorem and the duality theorem of linear programming is this “stictly feasible” condition in the theorem. Let’s proceed to the proof. As in the the LP proof the outline is the following: first we prove weak duality ( for feasible
) and then we consider the dual restrictions with
and we apply Farkas’ Lemma:
Proof: Weak duality: If is feasible for 1 and
is feasible for 2 then:
because and the
of two positive semi-definite matrices is non-negative. Now:
by 1. Therefore,
Strong duality: Clearly, the following problem has no solution:
where is the optimal value of 2. Now we apply the inomogeneous Farkas’ Lemma to:
and we get a matrix such that:
which means: and
. We know that
and
. We just need to prove that
. We already know it is not negative, so we need to prove it is not zero and here we will need the hypothesis that the dual has a strict solution. If
then there would be solution to:
and by Farkas’ Lemma, the problem:
would have no solution and we know it does have a solution. Therefore, .
Everything else comes from combining the weak and strong version described above.