Big Red Bits

More on eigenvalues and social networks

July 29th, 2009 renatoppl No comments

Following the suggestions of some of my friends, I decided to look at the other eigenvalues. The intuition is that if an eigenvalue is close to $1$ , it must also represent a good partition of the graph. Therefore I ploted the same graph as in my last post but associating each node $v$ with the coordinates $(x_3(v), x_n(v))$ where $x_i$ is the eigenvector corresponding to the $i$ -th eigenvalue. The first eigenvalues are actually very close to $1$ . 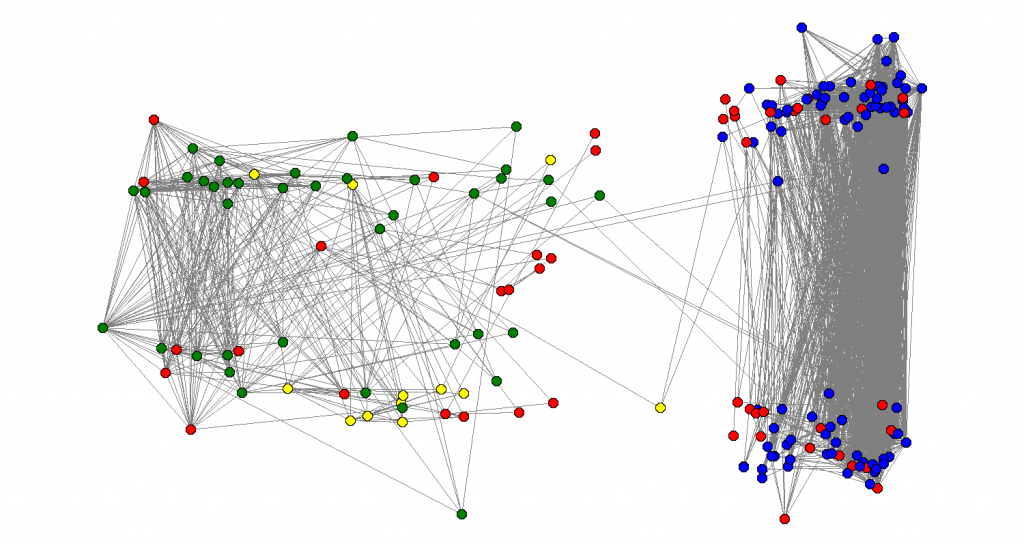I have: $\lambda_1 = 1.0$ (as expected), $\lambda_2 = 0.9925$ , $\lambda_3 = 0.9318$ , $\lambda_4 = 0.8596$ , $\lambda_5 = 0.8493$ , … For my suprise, plotting $(x_3(v), x_n(v))$ gave a nice and natural separation between the nodes representing people from my family (in yellow) and the other cathegories:

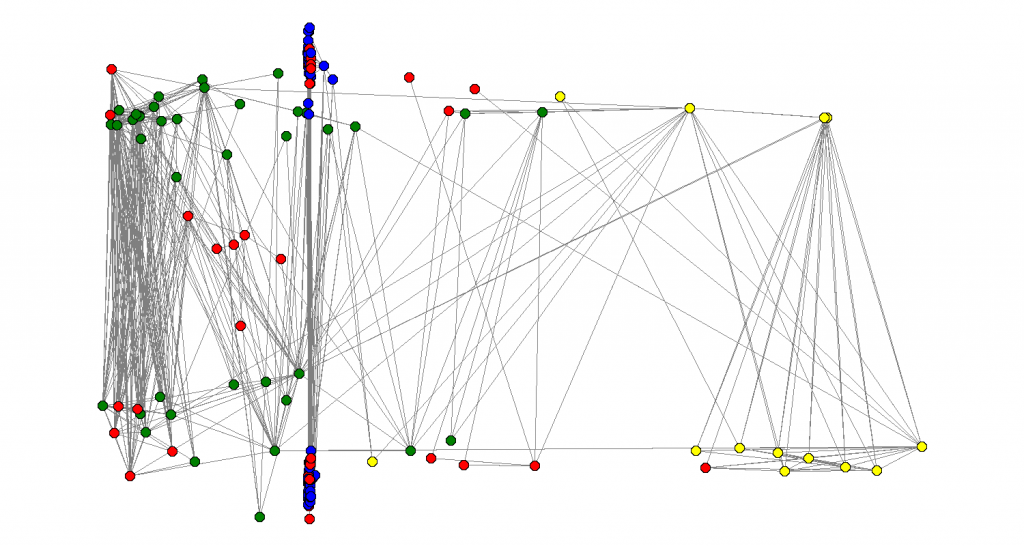orkut_l3_ln Also, I looked at this version of the graph with people names, and I noticed that people with extreme values of $x_2(v)$ are very good representatives of their respective clusters. In that first graph (in the other blog post), we got a good separation of my high-school friends (in green) and my undergrad friends (in blue). The nodes in the extreme right are my friends I used to hang out more with in college – they are people that are definitely in that cluster. The same about the friends in the extreme left, they are definitely in the other cluster.

Now, let’s turn our attention to the picture above. Not only the yellow nodes were clusterized, the blue nodes appear to be all in the same place, as if the main cluster identified in the last eigenvector all collapses to one point. If we look further at the fourth eigenvector, this phenomenon still happens:

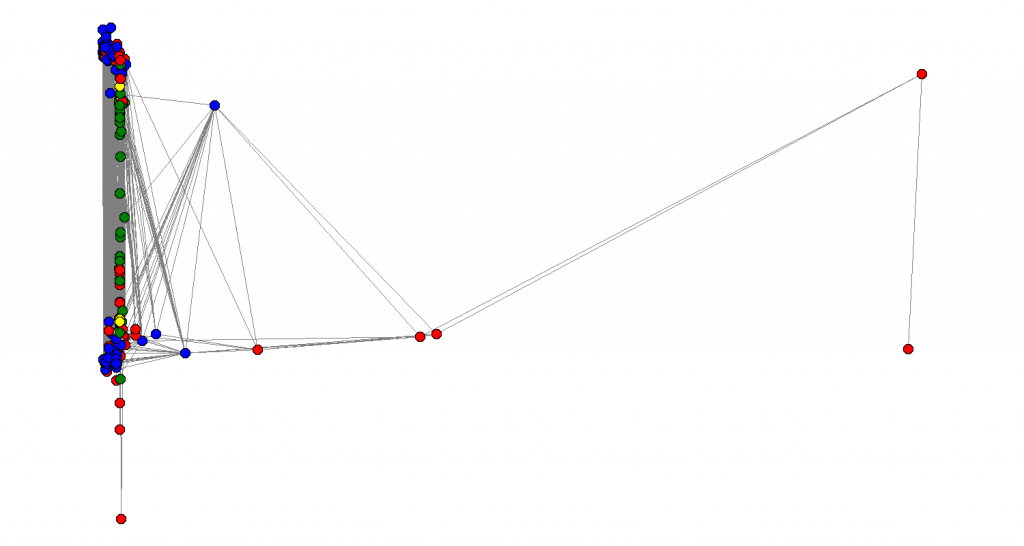orkut_l4_ln See how all the nodes that were somehow “important” in the last two graphs all collapse to the same place and now we are trying to sort the other nodes. How far can we go? Is there some clean recursive way of extracting multiple (possible overlapping) communities in those large graphs just looking in the local neighborhood? I haven’t reviewed much of the literature yet.

Eigenvalue density

I am also curious about how is the distribution of the eigenvalues of that graph. For example, the following graph shows the “eigenvalue density”. We know that $\lambda_i \in [-1,1]$ , but how are they distributed in this interval. The largest eigenvalue is $1$ and the smallest is $-0.7233$ . The next plot shows the distribution:

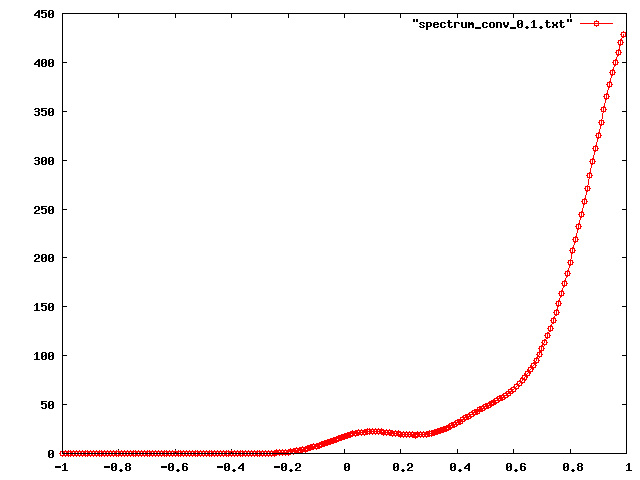eigenvalue_density Most of the eigenvalues are accumulated on the positive side (this graph really seems far from being bipartite). Another interesting question if: how can we interpret the shape of this curve. Which characteristics from the graph can we get? I still don’t know how to answer this questions, but I think some spectral graph theory might help. I really need to start reading about that.

Next, I plotted the points $(i, \lambda_i)$ in a graph and got the following pattern:

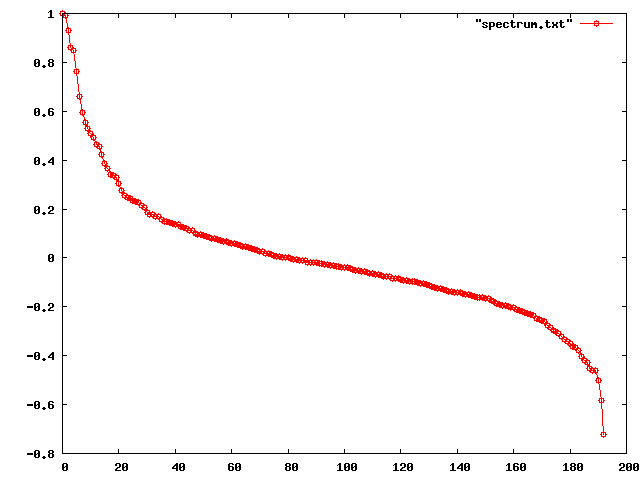spectrum This seems like a nice symmetric pattern and there should be a reason for that. I don’t know in what extent this is a property of real world graphs or from graphs in general. There is this paper by Mihail and Papadimitriou analyzing the structure of eigenvalues in real world graphs. They propose a model for explaining why the highest eigenvalues seem to be a power-law distribution, i.e. $\lambda_i = \frac{\lambda_1}{\alpha^i}$ for the first $k$ eigenvalues. They claim the eigenvalues are close to $\sqrt{d_i}$ where $d_i$ is the $i$ -th highest degree. Therefore, since $d_i$ follows a power law, $\lambda_i$ should also follow.

Although the whole social netwotk follows a power-law (more about power-laws in this nice survey by Mitzenmacher), we are dealing with a local neighborhood and even the degrees in the graph don’t follow a power law, as we can see in the following log-log plot of $(i, \sqrt{d_i})$ and $(i, \lambda_i)$ :

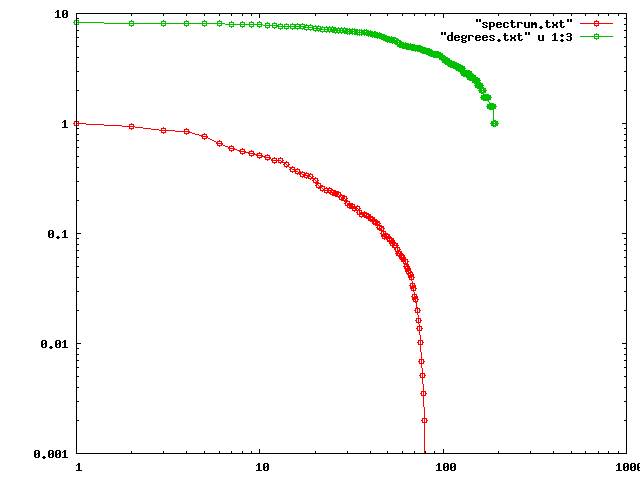spectrum_log Even though they are not a power-law, they still seem to have a similar shape, which I can’t exacly explain right now. Papadimitrou suggests that the fact that $\lambda_i \approx \sqrt{d_i}$ is a negative result, since $\lambda_i$ seems to be reflecting only a local property of the graph. Here it seems to be following a similar pattern, however, we saw that we can get some nice global and structural properties from that, so it doesn’t seem to be reflecting only local properties.

Categories: theory Tags: data, mining graphs, spectral theory, theory

Eigenvectors and communities

July 26th, 2009 renatoppl 2 comments

I liked a lot the talk by Luca Trevisan in STOC’09 about the “Max Cut and the Smallest Eigenvalue”. In this paper he proposes an ${.531}$ -approximation algorithm for MAX-CUT, which is the first approximation algorithm for MAX-CUT that doesn’t use semi-definite programming (SDP). The best possible approximation for that problem is the 0.878-approximation given by Goemans and Williamson, based on SDP (which is the best possible approximation assuming the Unique Games Conjecture).

I won’t discuss the paper in much detail here, but its heart is the very beautiful idea of analyzing properties of a graph looking at the spectrum of the matrix that defines it. For example, represent a graph ${G}$ by its adjacent matrix ${A}$ , i.e., ${A}$ is an ${n \times n}$ matrix (where ${n}$ is the number of nodes of ${G}$ ) and ${A_{ij} = 1}$ iff the edge ${(i,j)}$ is in ${G}$ . Let also ${D}$ be the diagonal matrix for which ${D_{ii}}$ is the degree of node ${i}$ . The normalized adjacency matrix is given by ${D^{-1/2} A D^{-1/2}}$ . Let ${\lambda_1 \geq \lambda_2 \geq \hdots \geq \lambda_n}$ be its eigenvalues. It is easy to see that all the eigenvalues are in ${[-1,1]}$ , since:

$\displaystyle 0 \leq \sum_{ij} A_{ij} (x_i - x_j)^2 = 2 x^t D x - 2 x^t A x \Rightarrow \frac{x^t A x}{x^t D x} \leq 1$

taking ${y = D^{1/2}x}$ we have that: ${\frac{y^t D^{-1/2} A D^{-1/2} y}{y^t y} \leq 1}$ for all ${y \in {\mathbb R}^n}$ . It is not hard to see the the maximum eigenvalue is:

$\displaystyle \lambda_1 = \max_{y \in {\mathbb R}^n} \frac{y^t D^{-1/2} A D^{-1/2} y}{y^t y}$

To prove ${\lambda_n \geq -1}$ it is analogous, just by analyzing ${\sum_{ij} A_{ij} (x_i + y_i)^2 \geq 0}$ . The next natural questions is: do those bounds hold with equality?

In fact, ${\lambda_1 = 1}$ for all graphs. It is very easy to see that, just take the vector ${x \in {\mathbb R}^n}$ with ${x_i = \sqrt{d_i}}$ where ${d_i}$ is the degree of node ${i}$ . And for ${\lambda_n}$ , it is not difficult to see that ${\lambda_n = -1}$ iff the graph has a bipartite connected component. It is also easy to see that if the graph has ${k}$ connected components then ${\lambda_1 = \hdots = \lambda_k = 1}$ .

So, given a connected graph ${\lambda_2 < 1}$ . But what happens if ${\lambda_2}$ is very close to ${1}$ . Intuitively, it means that the graph is almost disconnected in the sense that it has a very sparse cut. For ${d}$ -regular graphs (a graph where all nodes have degree ${d}$ ), this intuition is captured by Cheeger’s inequality.

$\displaystyle \sqrt{2 (1-\lambda_2) } \geq h_G \geq \frac{1}{2} (1-\lambda_2)$

where ${h_G}$ is the sparsity of ${G}$ , defined as ${\min_{S \subseteq V} \frac{\vert e(S, V \setminus S) \vert}{d \min\{\vert S \vert, \vert V \setminus S \vert \}}}$ . In the paper, Luca Trevisan discusses an analogue os Cheeger’s Inequality for the smallest eigenvalues ${\lambda_n}$ . Instead of measuring how close we are from a disconnected graph, we measure how close we are from a a bipartite graph.

Let’s try to get some intuition: if a ${d}$ -regular graph has a good sparse cut, like in the picture below, we could divide it in two parts and try to get an eigenvalue close to ${1}$ by the following way: set “almost” ${1}$ in one part and almost ${-1}$ in the other. Since there are very few edges crossing the cut, after being transformed by ${\frac{1}{d}A}$ the values are almost still the same. Also if the graph is almost bipartite, we can set almost ${1}$ in one part and almost ${-1}$ in the other, and after applying ${\frac{1}{d}A}$ , what was ${1}$ becomes ${-1}$ and vice versa.

eigenvalues

Ok, we can use eigenvalues to have a good idea if the graph has good expansion or not, but how to use that to actually find good partitions of it? Let ${x_2}$ be the eigenvector corresponding to ${\lambda_2}$ . The intuition in the last paragraph tells us that maybe we should think of getting ${S_1 = \{v \in V; x_2(v) < 0\}}$ and ${S_1 = \{v \in V; x_2(v) \geq 0\}}$ . More generally we can substitute ${0}$ by a threshold ${t}$ . This gives us only ${n}$ possible partitions to test and choose the best, instead of ${2^n}$ .

Finding Communities in Graphs

Real world graphs like social networks have clusters of nodes that can be identified as communities. There is a lot of work in finding those communities using all sorts of methods – more references about that can be found in Jon Kleinberg’s Networks course website. Spectral techniques are a natural candidate for doing that. I did a small experiment using Orkut, the most used social network in Brasil. Let ${G}$ be the entire graph of Orkut and ${u}$ be the node representing my profile on ${G}$ and let: ${\partial \{u\} = \{ v; (u,v) \in E(G)\}}$ be the set of all my friends and ${G[\partial \{u\}]}$ be the graph induced on my friends.

First, I crawled the web to reconstruct ${G[\partial \{u\}]}$ (notice I am not in the graph, so I am not using the fact that I am connecting all them. I am just using the connections between them). First, I have ${211}$ friends, which form a huge ${194}$ nodes component, and smaller components (one of size ${5}$ , two of size ${3}$ and six of size ${1}$ ). Let’s forget about the smaller components and care about the huge component: in this component there are my friends from undergrad, my friends from high-school, my family and some miscellaneous friends. Although all of them are interconnected, I wanted to be able to separate them just by using the topology of the graph.

I did the following experiment: I calculated the eigenvalues and eigenvectors of ${D^{-1/2} A D^{-1/2}}$ . Let ${1 = \lambda_1 \geq \hdots \lambda_n}$ be the eigenvalues and ${x_1, \hdots, x_n}$ be the eigenvectors. For each node ${v \in V}$ , I associated with coordinates ${(x_2(v), x_n(v))}$ in a way that a vertical cut would be a good approximation of the sparsest cut and an horizontal line would be a good approximation of the max-cut. The result is there:

orkut

After doing that I labeled the nodes of the graph with colors: my friends from IME (my undergrad university), I labeled blue. My friends from high-school, I labeled green, my family nodes, I labeled yellow and friends from other places, I labeled red. Also, there were some people that used strange characters in their names I could no parse, so I also labeled them red. I was happy to see that the algorithm efficiently separated the green from the blue nodes: clearly distinguishing between my high-school and my undergrad friends.

More about spectral methods

Luca Trevisan has a lot of very cool blog posts about Cheeger’s inequality and other interesting proofs of spectral facts. This MIT course has a lot of material about Spectral Graph Theory.

Categories: theory Tags: data, sparsest cut, spectral theory, theory

Archive

More on eigenvalues and social networks

Eigenvectors and communities

Recent Posts

Archives

Categories

Comics

Systems Links

Theory Links

Meta