Archive

Posts Tagged ‘theory’

Eigenvectors and communities

July 26th, 2009 2 comments

I liked a lot the talk by Luca Trevisan in STOC’09 about the “Max Cut and the Smallest Eigenvalue”. In this paper he proposes an {.531}-approximation algorithm for MAX-CUT, which is the first approximation algorithm for MAX-CUT that doesn’t use semi-definite programming (SDP). The best possible approximation for that problem is the 0.878-approximation given by Goemans and Williamson, based on SDP (which is the best possible approximation assuming the Unique Games Conjecture).

I won’t discuss the paper in much detail here, but its heart is the very beautiful idea of analyzing properties of a graph looking at the spectrum of the matrix that defines it. For example, represent a graph {G} by its adjacent matrix {A}, i.e., {A} is an {n \times n} matrix (where {n} is the number of nodes of {G}) and {A_{ij} = 1} iff the edge {(i,j)} is in {G}. Let also {D} be the diagonal matrix for which {D_{ii}} is the degree of node {i}. The normalized adjacency matrix is given by {D^{-1/2} A D^{-1/2}}. Let {\lambda_1 \geq \lambda_2 \geq \hdots \geq \lambda_n} be its eigenvalues. It is easy to see that all the eigenvalues are in {[-1,1]}, since:

\displaystyle 0 \leq \sum_{ij} A_{ij} (x_i - x_j)^2 = 2 x^t D x - 2 x^t A x \Rightarrow \frac{x^t A x}{x^t D x} \leq 1

taking {y = D^{1/2}x} we have that: {\frac{y^t D^{-1/2} A D^{-1/2} y}{y^t y} \leq 1} for all {y \in {\mathbb R}^n}. It is not hard to see the the maximum eigenvalue is:

\displaystyle \lambda_1 = \max_{y \in {\mathbb R}^n} \frac{y^t D^{-1/2} A D^{-1/2} y}{y^t y}

To prove {\lambda_n \geq -1} it is analogous, just by analyzing {\sum_{ij} A_{ij} (x_i + y_i)^2 \geq 0}. The next natural questions is: do those bounds hold with equality?

In fact, {\lambda_1 = 1} for all graphs. It is very easy to see that, just take the vector {x \in {\mathbb R}^n} with {x_i = \sqrt{d_i}} where {d_i} is the degree of node {i}. And for {\lambda_n}, it is not difficult to see that {\lambda_n = -1} iff the graph has a bipartite connected component. It is also easy to see that if the graph has {k} connected components then {\lambda_1 = \hdots = \lambda_k = 1}.

So, given a connected graph {\lambda_2 < 1}. But what happens if {\lambda_2} is very close to {1}. Intuitively, it means that the graph is almost disconnected in the sense that it has a very sparse cut. For {d}-regular graphs (a graph where all nodes have degree {d}), this intuition is captured by Cheeger’s inequality.

\displaystyle \sqrt{2 (1-\lambda_2) } \geq h_G \geq \frac{1}{2} (1-\lambda_2)

where {h_G} is the sparsity of {G}, defined as {\min_{S \subseteq V} \frac{\vert e(S, V \setminus S) \vert}{d \min\{\vert S \vert, \vert V \setminus S \vert \}}}. In the paper, Luca Trevisan discusses an analogue os Cheeger’s Inequality for the smallest eigenvalues {\lambda_n}. Instead of measuring how close we are from a disconnected graph, we measure how close we are from a a bipartite graph.

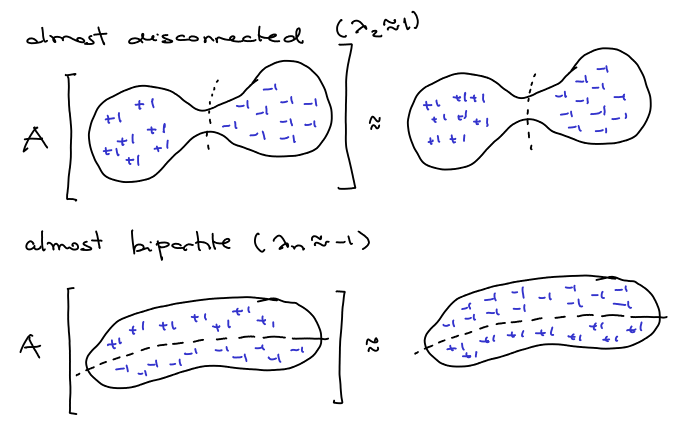
Let’s try to get some intuition: if a {d}-regular graph has a good sparse cut, like in the picture below, we could divide it in two parts and try to get an eigenvalue close to {1} by the following way: set “almost” {1} in one part and almost {-1} in the other. Since there are very few edges crossing the cut, after being transformed by {\frac{1}{d}A} the values are almost still the same. Also if the graph is almost bipartite, we can set almost {1} in one part and almost {-1} in the other, and after applying {\frac{1}{d}A}, what was {1} becomes {-1} and vice versa.

eigenvalues

Ok, we can use eigenvalues to have a good idea if the graph has good expansion or not, but how to use that to actually find good partitions of it? Let {x_2} be the eigenvector corresponding to {\lambda_2}. The intuition in the last paragraph tells us that maybe we should think of getting {S_1 = \{v \in V; x_2(v) < 0\}} and {S_1 = \{v \in V; x_2(v) \geq 0\}}. More generally we can substitute {0} by a threshold {t}. This gives us only {n} possible partitions to test and choose the best, instead of {2^n}.

Finding Communities in Graphs

Real world graphs like social networks have clusters of nodes that can be identified as communities. There is a lot of work in finding those communities using all sorts of methods – more references about that can be found in Jon Kleinberg’s Networks course website. Spectral techniques are a natural candidate for doing that. I did a small experiment using Orkut, the most used social network in Brasil. Let {G} be the entire graph of Orkut and {u} be the node representing my profile on {G} and let: {\partial \{u\} = \{ v; (u,v) \in E(G)\}} be the set of all my friends and {G[\partial \{u\}]} be the graph induced on my friends.

First, I crawled the web to reconstruct {G[\partial \{u\}]} (notice I am not in the graph, so I am not using the fact that I am connecting all them. I am just using the connections between them). First, I have {211} friends, which form a huge {194} nodes component, and smaller components (one of size {5}, two of size {3} and six of size {1}). Let’s forget about the smaller components and care about the huge component: in this component there are my friends from undergrad, my friends from high-school, my family and some miscellaneous friends. Although all of them are interconnected, I wanted to be able to separate them just by using the topology of the graph.

I did the following experiment: I calculated the eigenvalues and eigenvectors of {D^{-1/2} A D^{-1/2}}. Let {1 = \lambda_1 \geq \hdots \lambda_n} be the eigenvalues and {x_1, \hdots, x_n} be the eigenvectors. For each node {v \in V}, I associated with coordinates {(x_2(v), x_n(v))} in a way that a vertical cut would be a good approximation of the sparsest cut and an horizontal line would be a good approximation of the max-cut. The result is there:

orkut

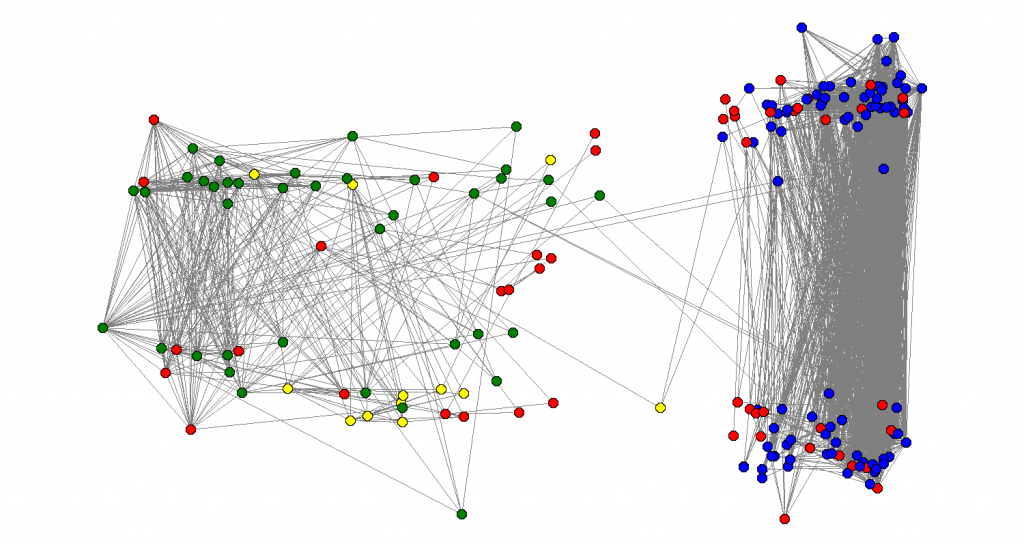
After doing that I labeled the nodes of the graph with colors: my friends from IME (my undergrad university), I labeled blue. My friends from high-school, I labeled green, my family nodes, I labeled yellow and friends from other places, I labeled red. Also, there were some people that used strange characters in their names I could no parse, so I also labeled them red. I was happy to see that the algorithm efficiently separated the green from the blue nodes: clearly distinguishing between my high-school and my undergrad friends.

More about spectral methods

Luca Trevisan has a lot of very cool blog posts about Cheeger’s inequality and other interesting proofs of spectral facts. This MIT course has a lot of material about Spectral Graph Theory.

Categories: theory Tags: , , ,

Submodularity

June 22nd, 2009 No comments

Last week a heard at least twice about submodularity what made me want to write about. First, it was in the talk by Carlos Guestrin in the first CompSust conference. His very interesting point was: Machine Learning explored Convexity in the core of many machine learning algorithm (SVMs, for example). We should look for other general models, other than convexity, that have interesting properties and so that we could design algorithms based on that. He proposes submodularity as a natural candidate.

The idea of submodular functions generalizes in a certain way the concept of concave functions. The main property captured is the disminishing returns property. Consider a set {S} and the set {2^S} of its subsets. We say that a function {f: 2^S \rightarrow \mathbb R} is submodular if:

\displaystyle f(S \cup \{z\}) - f(S) \geq f(T \cup \{z\}) - f(T) \text{ for } S \subseteq T

that is, adding a new element {z} to a larger set has smaller marginal gain than adding it to a smaller set. This is very natural in a lot of circumstances: for example, let {S} be a set of books (or papers) anf {f(S)} be the knowledge you get by reading each of them. Since the topics overlap, reading an extra book when you already read {100} has a smaller marginal gain (or at least no greater) than reading it when you read only {10}. One can think of it as a natural generalization of concave functions, which also have this disminishing returns propery. Actually if {\phi} is a concave function, {f(S) = \phi(\vert S \vert)} is submodular.

In the Cascading Behavior in Networks, Jon Kleinberg described a very interesting submodular function: considere a graph {G = (V,E)} and a epidemia spreading through the nodes. Suppose an initial set {S \subseteq V} of infected nodes. As soon as one node {u} becomes infected, each node {v}, s.t. {(u,v) \in E} becomes infected with probability {p}. Let {f(S)} be the expected number of infected nodes in the end. It can be proved that {f} is submodular. One can think of this infection as being some information spreading in a network (say, the blogosphere). Then, if we start spreading this information through {k} nodes, which nodes should we pick to make sure most nodes will get the information in the end?

Another example is vertex cover: we can think of {S \subseteq V} as a set of nodes in a graph and {f(S)} the number of edges covered by those nodes. It is nor hard to see that this function is submodular. Set cover and other covering problems can be modelled as submodular functions. Normally, the main question is something like: how can I maximize {f} given that I can pick at most {k} elements for {S}, or, stated in mathematical terms:

\displaystyle \max_{\vert S \vert \leq k} f(S)

The fact that {f} is submodular makes it easy to approximate it using a greedy algorithm, using the following very interesting result:

Theorem 1 (Nemhauser et al, 78) Given a monotonic (i.e {f(S) \leq f(T)} for {S \subseteq T}) submodular function {f : 2^X \rightarrow {\mathbb R}_+} with {f(\emptyset) = 0}, the set {S = S_k} obtained by taking {S_0 = \emptyset} and

\displaystyle S_{i+1} = S_i \cup \{z_i\} \text{ where } z_i \in \text{argmin}_{z \notin S_i} f(S_i + z)

is a {\left( 1 - \frac{1}{e} \right)} approximation to {\max_{\vert S \vert \leq k} f(S)}.

Proof: First, notice that:

\displaystyle \begin{aligned}f(A \cup B) & = \sum_{j=1}^n f(A \cup \{b_1, \hdots, b_j \}) - f(A \cup \{b_1, \hdots, b_{j-1} \}) \\ & \leq \sum_{j=1}^n f(A \cup \{b_j \}) - f(A) \end{aligned}

where the last part follows by submodularity. Let {T} be the optimal solution for the problem, so we have that:

\displaystyle f(T) \leq f(S_i \cup T) \leq f(S_i) + \sum_{t \in T} f(S_i \cup \{ t \}) - f(S_i) \leq f(S_i) + \sum_{t \in T} f(S_{i+1}) - f(S_i)

because of our choice of {z_i}. So, if {\delta_i = f(S_i) - f(S_{i-1})} then we know that:

\displaystyle f(T) \leq f(S_i) + k \delta_{i+1} \Rightarrow \delta_{i+1} \geq \frac{f(T) - f(S_i)}{k}

and therefore:

\displaystyle f(S_{i+1}) = f(S_i) + \delta_{i+1} \geq \frac{1}{k} f(T) + \left( 1 - \frac{1}{k} \right) f(S_i)

Solving that recursion, it is easy to see that:

\displaystyle f(S_i) \geq \left[ 1 - \left( 1 - \frac{1}{k} \right)^i \right] f(T)

what gives the {1-1/e} bound.\Box

The second time I heard about submodularity last week was in a nice talk in the Theory Discussion Group about the paper Approximating submodular functions everywhere. Basically there is a monotone submodular function {f:2^{[n]} \rightarrow \mathbb R}. The values of {f(S)} are calculated through an oracle. The paper shows how to construct a function {\hat{f}(S)} that approximated {f(S)} everywhere just by calling the oracle a {poly(n)} number of times. The approximation is such that:

\displaystyle \hat{f}(S) \leq f(S) \leq \tilde{O}(\sqrt{n}) \hat{f}(S)

The paper is very deep, so I will not comment about it, but about some nice things I learned in the introduction of the talk about submodular functions and polymatroids. The polymatroid is the following polyhedron associated with a submodular function:

\displaystyle P_f = \left\{ x \in {\mathbb R}_+^n; x(S) \leq f(S), \forall S \subseteq [n] \right\}

where {x(S) = \sum_{i \in S} x_i}.

One nice thing about those objects is that we can easily optimize over them using a greedy algorithm:

Theorem 2 Considere a weight function {w:[n] \rightarrow {\mathbb R}_+} and a monotone submodular function {f:2^{[n]} \rightarrow {\mathbb R}_+}. Then the problem:

\displaystyle \min_{x \in P_f} \langle w, x\rangle

can be solved by the following greedy algorithm: order the elements in the set according to the {w}-value, i.e, {[n] = \{ s_1, \hdots, s_n\}} with {w(s_1) \geq w(s_2) \geq \hdots \geq w(s_n) } and define

\displaystyle x(s_i) = f(\{s_1, \hdots, s_i\}) - f(\{s_1, \hdots, s_{i-1}\})

Proof: We need to prove that {x} is a feasible point of {P_f} and then that {x} is optimal. To prove feasibility, we need to prove that for all {U \subseteq [n]} we have {x(U) \leq f(U)}. We prove for all sets {U \subseteq \{ s_1, \hdots, s_i \}} for all {i} and we do that by induction in {i}. For {i = 0}, it is trivial. Then, supposing we proved for {i}, let’s prove for {i+1}. Take {U \subseteq \{ s_1, \hdots, s_{i+1} \}}. If {s_{i+1} \notin U}, we are done. If not:

\displaystyle \begin{aligned} x(U) & = x(U \setminus \{ s_{i+1} \}) + x(s_{i+1}) \\ & \leq f(U \setminus \{ s_{i+1} \}) + f(\{s_1, \hdots, s_{i+1}\}) - f(\{s_1, \hdots, s_{i}\}) \leq f(U) \end{aligned}

Now, we need to prove optimality and this is essentially a primal-dual argument. The dual of the linear program:

\displaystyle \min \langle w, x\rangle \text{ s.t. } x(U) \leq f(U); x(U) \geq 0; \forall U \subseteq [n]

if the program:

\displaystyle \max \sum_{U \subseteq [n]} f(U) y(U) \text{ s.t. } \sum_{U; i \in U} y(U) \geq w_i; \forall i \in [n]; y(U) \geq 0

Consider the following dual solution: {y(\{s_1, \hdots, s_i\}) = w_i - w_{i+1}} (take {w_{n+1} = 0}) and {y(U) = 0} for all other sets. It is clearly feasible and matches the objective value of the primal solution. Both are therefore optimal. \Box

Notice that the proof has a “matroid flavour” and there is where the name poly-matroid comes from. Note that the rank function of a matroid is a submodular function and that the polymatroid of the rank function is something called the independent set polytope of the matroid. More about it in a later blog post.

Categories: theory Tags: , , ,